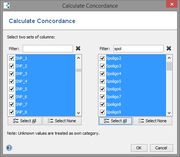
Calculate the concordance (Rand's and Wallace's Coefficients) between two sets of columns. This function can be used to compare the results of different typing systems.
For calculation, pairs of the results of 2 typing systems <math>(x,y): x,y \in {Samples}</math> of all Samples are created. All pairs are arranged in a 2x2 table, according to their type in both typing systems:

The ratio <math>\frac{(A+D)}{A+B+C+D}</math> is the frequently called in publications the typing system concordance. This value is also known as Rand's coefficient.
However, if comparing two random data sets, concordance calculation does not approach the value 0. Therefore, when calculating the Adjusted Rand coefficient, a correction factor is used to take into account the presence of chance agreement:
Adjusted Rand = <math>\frac {A+D-n_c}{A+B+C+D-n_c}</math> with
<math>n_c = \frac {n(n^2+1) - (n+1) \sum n_i^2-(n+1) \sum n_j^2+2 \sum \sum n_c = \frac {n_i^2 n_j^2}{n}}{2(n-1)}</math>
where <math>n</math> represents the total number of Samplesand <math>n_i, n_j</math> represent the numbers of Samples with values <math>i</math> and <math>j</math> for System 1 and System 2.
Wallace's coefficients are calculated by
<math>W_1 = \frac {A}{A+B}</math> and
<math>W_2 = \frac {A}{A+C}</math>
They represent the probability that a pair of Samples that have the same type in System 1 also have the same type in System 2 and vice versa. See [Carriço et. al. 2006].
Unknown values are treated as own category.
References
Carriço J.A., Silva-Costa C., Melo-Cristino J., Pinto F.R., de Lencastre H., Almeida J.S., Ramirez M.: Illustration of a common framework for relating multiple typing methods by application to macrolide-resistant Streptococcus pyogenes., J. Clin. Microbiol. 44:2524-32, 2006
FOR RESEARCH USE ONLY. NOT FOR USE IN CLINICAL DIAGNOSTIC PROCEDURES.